서론
현재 교통, 국방, 의료, 재난현장 등 여러 분야에서 RADAR를 사용하고 있다. 특히 점점 더 발전하고 있는 자율주행 기술에도 이 레이더 기술이 활용되고 있다.
따라서 이후에 이 RADAR를 활용해보고 싶어 관련 지식을 공부하며 블로그 글로 정리하려고 한다.
RADAR란?
RADAR : RAdio Detecting And Ranging 의 줄임말.
풀어 해석하자면 “전파를 이용해 물체를 탐지하고 거리를 측정” 하는 것이다.
하지만 이 레이더를 활용 시 탐지와 거리측정 뿐만 아니라 물체의 방향, 각도, 속도도 얻을 수 있고, 처리를 거치면 영상이나 이미지 역시 얻을 수 있다.
안테나 형태에 따른 분류
레이더는 안테나의 형태에 따라 분류할 수 있다.
- 단일 안테나 레이더 (단상태, Monostatic)
하나의 안테나로 송/수신을 같이 한다. 송수전환기(Duflex)를 이용해 송신 및 수신 신호를 구분한다.
- 이중 안테나 레이더 (쌍상태, Bi-static)
송신용 안테나와 수신용 안테나가 분리되어 있다.
- 다중 안테나 레이더 (Multi-static)
송신기 하나에 여러 수신기로 구성된 것을 말한다.
레이더 반사면적 (Radar Cross Section, RCS)
레이더는 “전자기파의 속도는 빛의 속도와 같고 빛의 속도는 일정하다”는 원리로 물체와의 거리를 측정한다.
이런 법칙에 따라 전파를 송신 후 물체에 반사되어 나온 전파를 수신해 둘의 시간 차이를 알 수 있다면 안테나와 목표의 거리를 알 수 있다.
반사되는 목표물은 비행기, 배와 같은 큰 물체부터 새, 빗방울과 같이 작은 물체까지 크기가 다앙하고,
이러한 목표물의 크기, 구조, 재질 등 에 따라 반사되어 되돌아오는 반사파의 파워가 달라진다.
이렇게 레이더 전파가 물체에 닿아 반사될 때 레이더 수신기 방향으로 얼마나 잘 반사되는가를 면적으로 나타낸 척도가 RCS이다.
RCS의 경우 $\sigma$ (sigma) 기호를 주로 사용하며, 단위는 $m^2$이다.
RCS값이 $1m^2$이라면 정면 투영 단면적이 $1m^2$인 완전 반사되는 금속 구체의 반사 정도와 동일하다는 얘기다.
$1m^2$의 평판의 반사면적이 아니다!
평판의 경우, 레이더 전파의 입사각, 파장 길이에 따라 반사 면적이 크게 변화하며, 정면에서 수직으로 레이더가 조사되었을 경우 RCS는 대체로 자신의 면적보다 훨씬 크게 측정된다.
파장 = 3cm 인 X밴드 레이더 전파가 정면에서 수직 조사 시
한변의 길이가 0.3m인 정사각형 평판의 RCS = $113m^2$
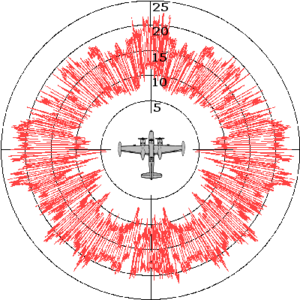전형적인 RCS 다이어그램 (B-26 Invader) [출처 : 위키백과]
위 사진에서 볼 수 있듯이 약간의 방위각 변화에도 측정치가 엄청나게 요동치는 것을 볼 수 있다.
15dB, 즉 거의 30배 수준으로 변화하다 보니 RCS 수치는 통계적으로 접근해야 한다.
일반적으로 전방위에서 RCS값을 모두 측정한 뒤 평균값 or 중간값을 표시한다. 그러나 스켈스 전투기가 등장하면서 마케팅의 일환으로 전면 RCS를 내세우는 경우가 많아졌다.
대부분의 비행기들은 전면 RCS가 다른 각도보다 훨씬 작게 측정되기 때문.
따라서 전면 RCS값 사용 시 훨씬 작은 숫자가 나오게 된다.
실제 우리가 사용하는 물품들이나 차량, 배, 비행기 등과 같은 운송 수단의 경우 단순한 평판이나 구형 물체에 비해 구조가 훨씬 복잡하고, 물체 자체의 전파 투과율이나 흡수율, 전파의 파장까지도 변수로 작용히기 때문에 실제 물체의 RCS를 쉽게 예측할 수는 없다.
물론 컴퓨터의 발전과 시뮬레이션의 발명으로 관련 소프트웨어도 존재하고 단순한 형태를 가진 물체의 RCS는 계산으로 구할 수도 있다. 하지만 이는 주어진 형상의 RCS를 예측하는 수준에 그치고,스텔스를 위한 최적의 형상을 찾는 것은 난이도가 높으며 그 대상이 비행기일 경우는 난이도가 수직상승한다.
스텔스 기술과 군사 항공기의 RCS값이 최고급 군사 기밀인 이유…
레이더 사용 시에도 많은 공부가 필요하다…😢
카메라 / LiDAR / RADAR 간의 장단점
흔히 사용하는 카메라와는 다르개 날씨와 조명의 영향을 받지 않아 기상상황 등에 상관 없이 사용할 수 있다는 장점이 있고, 카메라 / RADAR / LiDAR 등 여러 센서와 융합하여 사용하기도 한다.
각 센서의 장단점에 대해 비교하자면 아래와 같다.
| 카메라 | LiDAR | RADAR | |
|---|---|---|---|
| 가격 | 👍 | 👎 | ➖ |
| 정확성 | 👎 | 👍 | 👎 |
| 가시성 | ➖ | ➖ | 👍 |
| 날씨 변화 둔감성 | 👎 | ➖ | 👍 |
| 조명 둔감성 | 👎 | 👍 | 👍 |
| 공간 해상도 | 👍 | ➖ | 👎 |
RADAR의 경우 강한 전자기파를 송신하고 그것이 물체에 맞아 되돌아 오는 전자파를 분석해 대상의 위치정보(거리, 속도, 방향 등)를 측정한다.
이러한 전자기파를 송신하기 위해서는 안테나가 필요한데 전자파를 송신하는 방식에 따라 CW(연속파 레이더)와 PW(펄스파 레이더)로 나뉜다.
Pulse Wave RADAR
펄스 레이더는 레이더 송수신 신호로 Pulse Wave를 사용한다.
레이더를 송신 후 반사된 전파가 수신되기까지의 시간을 측정하여 물체까지의 거리를 계산할 수 있고,
2개 이상의 Pulse wave를 이용 시 물체의 변위와 시간차를 알 수 있으므로 속도를 계산할 수 있댜.
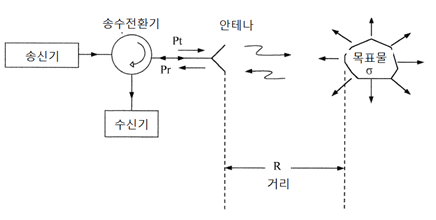펄스 레이더 다이어그램 [출처 : Radar 센서]
위 그림과 같이 하나의 안테나를 사용해 내부 Duplex를 활용하여 송수신 신호를 시간에 따라 분리해낸다.
따라서 송수신을 동시에 진헹하는 것이 아니다.
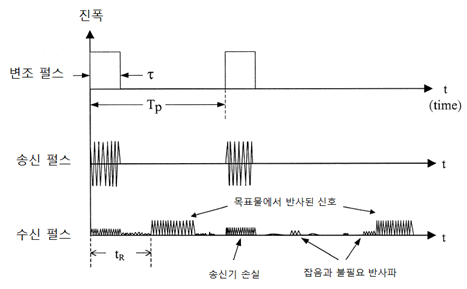펄스 레이더 신호 [출처 : Radar 센서]
거리 R의 경우 아래 식으로 구할 수 있다. (c = 빛의 속도) \[R=\frac{1}{2}ct_R\]
위 레이더에서 신호가 수신되기 전에 다음 Pulse wave를 송신한다면 거리 측정에 혼란이 발생 할 수 있다.
이를 막기 위해 $T_p$는 측정을 원하는 거리 R에 영향을 미치는 최대 $t_R$을 고려하여 이보다는 길게 설정해 주어야 하고, 혼란을 피하기 위한 최대 측정 거리는 아래와 같다. \[R_{max} = \frac{cT_p}{2} = \frac{c}{2f_p}\]
보통 $f_p$의 경우 100Hz ~ 100000Hz 정도로 설정하여 사용한다.
펄스 신호 2개를 거쳐서 거리를 얻어낸다면 물체의 변위와 시간차 역시 얻을 수 있으므로 속도도 계산할 수 있으나 기본적으로 펄스 레이더는 거리만 측정한다.
아래에서 소개할 도플러 효과와 펄스 신호를 합쳐서 속도와 거리 모두 얻을 수 있는 펄스 도플러 레이더도 있다.
Continuous Wave RADAR
연속파 레이더는 도플러 효과(Doppler Effect)를 활용해 물체의 속도를 얻기 때문에 도플러 레이더라고도 불린다.
도플러 효과
💡 도플러 효과 (Doppler Effect)
파동원과 관찰자의 상대 속도에 따라 진동수와 파장이 바뀌는 현상.
소리와 같이 매질을 통해 움직이는 파동에서는 관찰자와 파동원의 매질에 대한 상대속도에 따라 효과가 변한다.
그러나 빛이나 일반상대성이론에서의 자기력과 같이 매질이 필요 없는 파동의 경우
관찰자와 파동원의 상대속도만이 도플러 효과에 영향을 미친다. \[f’ = \left( \frac{v + v_0}{v - v_s}\right)f\] $f$: 파동의 실제 진동수, $f’$: 관찰자가 관측한 진동수, $v$: 파동의 매질 내에서 속도
$v_s$: 매질에 대한 파원의 속도 (파원이 관측자 쪽으로 움직일 때 양수),
$v_0$: 매질에 대한 관측자의 속도 (관측자가 파원 쪽으로 움직일 때 양수)
전자기파나 빛의 경우 관측자, 파원에 비해 속도가 훨씬 크므로 1차 근사치로 아래 식을 사용할 수 있다.
- 파원과 관측자가 전파 속도에 비해 매우 느리거나,
- 파원과 관측자의 거리가 전파의 파장에 비해 매우 큰 경우 유용하게 사용된다.
관측되는 주파수 $f$, 방출되는(파원의) 주파수 $f_0$, 방출되는(파원의) 파장 ${\lambda_0}$
관측되는 주파수 \[ f = \left( 1-\frac{v_{s,r}}{c}\right)f_0 \] 주파수의 변경 \[ \Delta f=-\frac{v_{s,r}}{c}f_0=-\frac{v_{s,r}}{\lambda_0} \]
여기서, $ v_{s,r} = v_s - v_r $ 즉, 관측자에 대한 파원의 속도
파원이 관측자 쪽으로 이동할 경우 음의 값, 멀어질 경우 양의 값을 가진다.
연속파 레이더란?
연속파 레이더의 경우 펄스 레이더와 달리 수신기가 신호를 받는 중에도 송신신호를 지속적으로 보내고,
펄스 변조가 필요없으므로 펄스 레이더에 비해 상대적으로 간단하다.
또힌 한개의 안테나를 사용할 경우 연속파 레이더는 송수신이 동시에 동작하므로
송신기의 잡음이 수신기 쪽으로 전이되어 수신기의 민감도를 떨어뜨릴 수 있다.
따라서 출력 파워를 송신기와 수신기 사이 간섭이 발생하지 않는 정도로 제한하고,
이로 인해 연속파 레이더는 주로 짧은 거리용으로 사용된다.
두 개의 안테나 시스템을 사용하면 송신기와 수신기 사이의 분리를 통해 거리를 늘릴 수 있긴 하나,
시스템이 매우 복잡해진다.
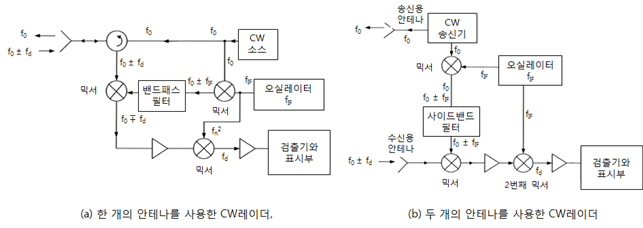연속파 레이더 다이어그램 [출처 : Radar 센서]
연속파 레이더는 도플러 효과로 인한 진동수의 변화로 파동원과 관찰자의 상대속도를 얻을 수 있지만, 연속적인 파형을 송신하므로 신호가 수신될 때까지 걸리는 시간 정보를 알 수 없어서 물체와의 거리는 확인할 수 없다.
이러한 단점을 보완한 것이 주파수 변조형 연속파 레이더(Frequency Modulated CW RADAR, FMCW 레이더)이다.
FMCW RADAR
물체와의 거리 측정을 위해서는 전파가 되돌아오기까지 걸린 시간 정보가 필요하다.
시간 정보를 송신하려면 진폭 변조, 주파수 변조, 위상 변조 등 변조가 필요한데, FMCW 레이더는 이 시간정보를 얻기 위해 CW레이더에 주파수 변조를 적용한 것이다.
자율 주행 자동차 등에서 가장 많이 사용되는 방식 중 하나이다.
LFM 파형 (Chirp 파형)
FMCW는 기본적으로 Chirp(Linear Frequency Modulation, LFM) 파형를 생성한다.
이는 주파수가 선형적으로 모듈레이션되는 파형이다. 새의 짹짹 소리의 주파수가 LFM파형과 유사하다고 해서 Chirp이라고 부르기도 한다. 주파수를 2차 함수 등의 형태로 변화시키는 Nonlinear Frequency Modulation 도 있다.
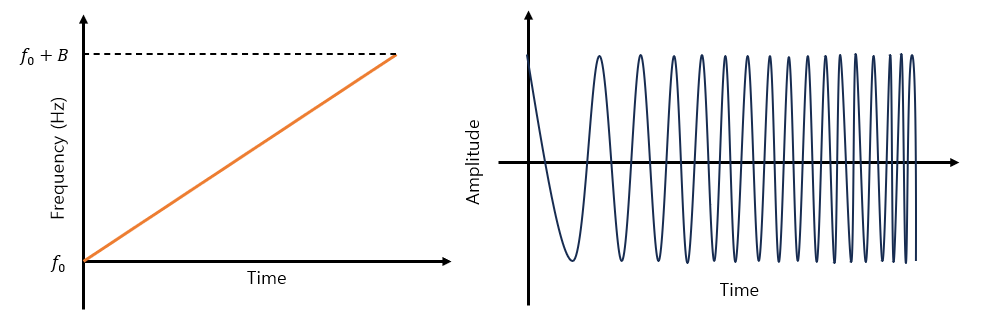LFM 파형 그림
FMCW RADAR 작동방식
위에서 언급한 바와 같이 FMCW는 시간정보를 얻기 위해 주파수 변조를 적용한 것이고, 따라서 시간은 송신 신호와 수신 신호 사이의 주파수 차이로부터 얻을 수 있다.
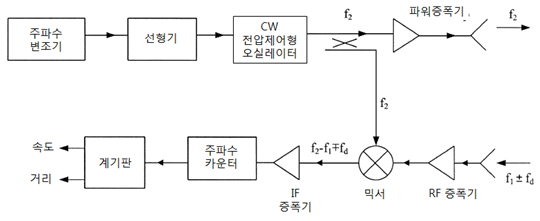FMCW 레이다의 블록선도 [출처 : Radar 센서]
위 블록선도는 2개의 안테나가 설치된 경우이다.
실제로는 Digital 신호를 Analog로 바꿔주는 DAC단이 있고 변환 시에 sampling rate에 따라 다양한 harmonic 성분을 갖기 때문에 이를 제거하기 위한 LPF(Low Pass Filter)를 거친다. 적절히 증폭된 뒤에 Carrier 주파수를 실어 주고 원치 않는 신호를 제거 하기 위해 BPF (Band Pass Filter)를 거친 후 증폭되어 안테나를 통해 전송된다. 표적에 반사된 신호는 수신 안테나를 통해 획득된다. 신호는 적절히 증폭된 뒤 Carrier 주파수가 제거된 뒤 Filtering을 거쳐 Digital로 변환되어 표적의 거리를 알 수 있도록 하는 신호처리를 거친다.
출처 : [레이더 시스템 설계 및 검증] LFM(chirp) 파형 Pulse compression (Convolution 방법)
위 블록선도에서 되돌아온 신호는 $f_1 \pm f_d$인데 +의 경우 목표물이 접근하고 있는 것이고 -의 경우 목표물이 멀어지고 있다는 것을 의미한다.
물체가 정지한 경우와 물체가 움직이는 경우 두가지로 나누어서 설명하겠다.
1️⃣ 물체가 정지해 있는 경우 (상대속도 = 0)
이 경우에는 도플러 효과가 발생하지 않으므로 $f_d = 0$ 이다.
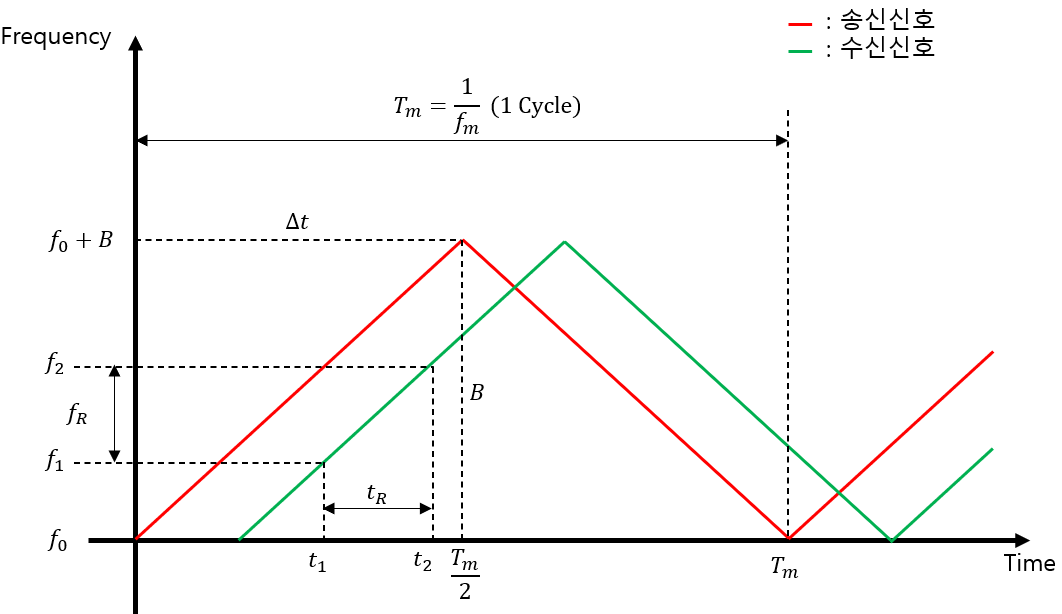물체 정지한 경우 그래프 [출처 : Radar 센서]
레이더 신호가 LFM이라면 위 그래프와 같이 주파수가 선형적으로 변하게 되는데 이 경우 수신기에서 받은 신호는 점선과 같다.
$t_1$에서 송신한 $f_1$주파수는 $t_2$에서 수신하게 되는데, 이때의 송신 주파수는 $f_2$로 변하게 된다. 블록선도에서 볼 수 있듯이 수신된 신호$f_1$은 수신 시 송신한 신호인 $f_2$와 믹서를 통해 혼합되게 되고, 이는 송신 주파수와 수신 주파수의 차이인 비트 주파수$f_b$를 생성한다.
💡 비트 주파수 (Beat Frequency)
FMCW 레이더 시스템에서 \[ \frac{B}{\Delta t}t_R - f_d \] 를 비트 주파수라고 하며 송신 신호와 수신 신호의 주파수 차를 이야기한다.
앞부분의 거리에 의한 지연시간 성분($f_R$)과
뒷부분의 속도 차이로인한 도플러 주파수 성분($f_d$)으로 이루어져있다.
이 경우 비트 주파수는 $f_2-f_1$이 된다. 물체가 정지해 있으므로 비트 주파수는 거리요소만 가지고 있다. 따라서 $f_R = f_b = f_2 - f_1$ 이 된다.
거리 $R$을 구하기 위해서는 위 그래프에서 송신신호와 수신신호의 주파수 차이, 전자기파의 속도(c), 그래프의 기울기를 알아야 한다. 레이더 시스템을 다자인할 때 주파수의 변화는 알고 있으므로 $\Delta f$ (진폭) 와 $f_m$ (진동수, 주기)은 알고있는 값이다. 따라서 그래프의 기울기를 알 수 있으므로 수신시간 $t_2$에서 비트 주파수인 $f_b$만 측정하면 물체까지의 거리를 알 수 있다.
\[ R = \frac{c t_R}{2} \] \[ t_R : f_R = \frac{1}{2f_m} : B \] \[ t_R = \frac{f_R}{2f_m B} \] \[ \therefore R = \frac{c f_R}{4 f_m B} \]
2️⃣ 물체가 움직이는 경우 ($f_d \ne 0$)
이 경우에는 물체의 움직임으로 인해 상대속도가 발생하여 도플러 효과가 비트 주파수에 포함되는 경우가 된다. 따라서 도플러 효과로 인한 속도 정보와 거리 정보를 분리해야 한다.
위에서 기술한 비트 주파수 식을 다시 써보면 \[ f_2 - f_1 - f_d \] 와 같은데, 여기서 $f_d$ 가 양수일 경우 물체가 레이더에 가까워지고 있는 것이고,
$f_d$ 가 음수일 경우 물체가 레이더로부터 멀어지고 있는 것이다.
레이더에 물체가 가까워지는 상황에서의 파형을 그려보면 아래와 같다.
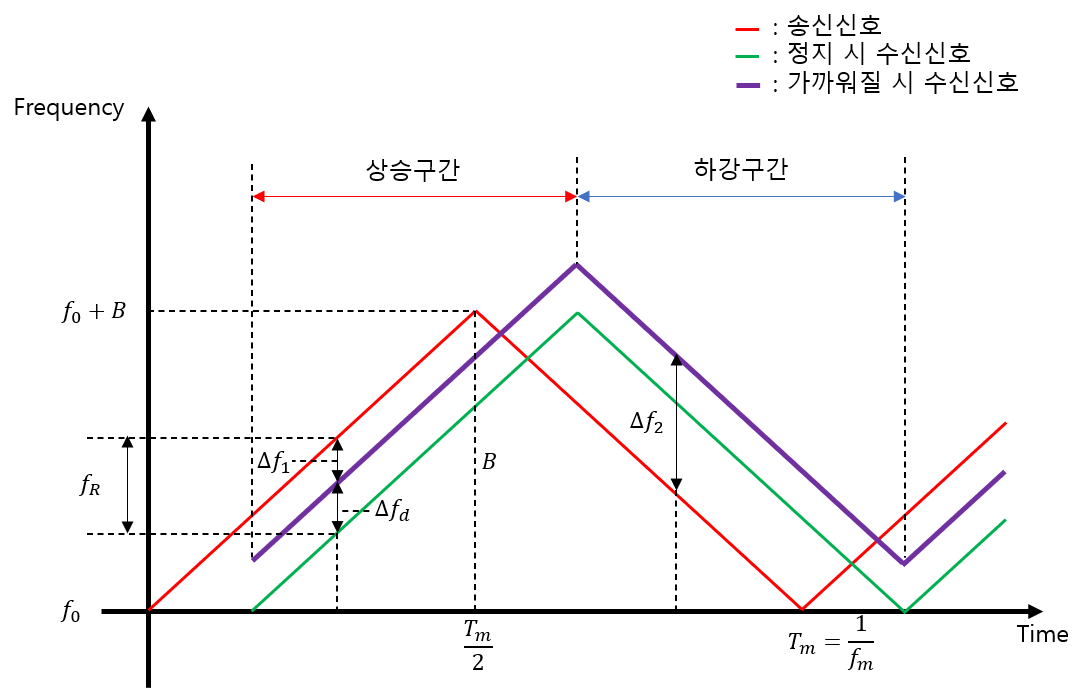물체가 움직일 때 파형 그래프
물체 정지 시에 거리 식을 $f_R$에 대해 다시 써보면 아래와 같다. \[ f_R = \frac{4R f_m B}{c} \]
또한 도플러 효과에 나온 주파수의 변경 식을 활용해서 $f_d$를 표현할 수 있는데,
위키백과 상에서 설명하는 도플러 효과는 파원에서 관측자로 오기만 하는 즉, 편도 경로에서의 식이다. 그러나 레이더의 경우 물체에서 반사되어 나오는 파장을 관측하는 것이므로 왕복 경로가 된다.
따라서, 위 “주파수의 변경” 식에 2를 곱해주어야 한다.
또한, 레이더의 경우 파원이 곧 관측자이고, 관측자에게 이동하는 물체의 속도를 측정하는 것이므로 부호 역시 바뀌어야 한다.
\[ f_d = \frac{2 v_r}{c}f_0 =\frac{2 v_r}{\lambda_0} \] $f_0$ = 송신한 진동수, $\lambda_0$ = 송신한 파장, $v_r$ = 물체의 상대속도
상승 구간에서의 주파수 차이 $ \Delta f_1 $ \[ \Delta f_1 = f_R - \Delta f_d = \frac{2}{c}(2R f_m B - f_0 v_r) \]
하강 구간에서의 주파수 차이 $ \Delta f_2 $ \[ \Delta f_2 = f_R + \Delta f_d = \frac{2}{c}(2R f_m B + f_0 v_r) \]
위 두 식을 빼주면 상대속도를 구할 수 있다. \[ \Delta f_2 - \Delta f_1 = \frac{4}{c}f_0 v_r \] \[ \therefore v_r = \frac{c}{4f_0}(\Delta f_2 - \Delta f_1) \]
위 두 식을 더할 경우 거리도 구할 수 있다. \[ \Delta f_2 + \Delta f_1 = \frac{8R f_m B}{c} \] \[ \therefore R = \frac{c}{8R f_m B}(\Delta f_2 + \Delta f_1) \]
물체 위치의 각도 구하기
지금까지 기술한 공식들로 물체의 거리와 상대속도를 모두 구할 수 있다. 그러나, 거리만 알고 있을 경우 레이더 반경에 포함되는 모든 거리상에 물체가 존재할 수 있다는 얘기가 된다. 따라서, 물체의 위치를 정확히 특정하기 위해서는 물체의 각도를 알아야 한다.
우리가 흔히 사용하는 레이더 센서에는 송신 안테나와 수신 안테나 하나씩 붙어있는 것이 아니고, 각각의 안테나가 여러개가 붙어있다. TI 사의 AWR1843AOPEVM 제품 User guide 사진을 예로 들면 아래와 같다.
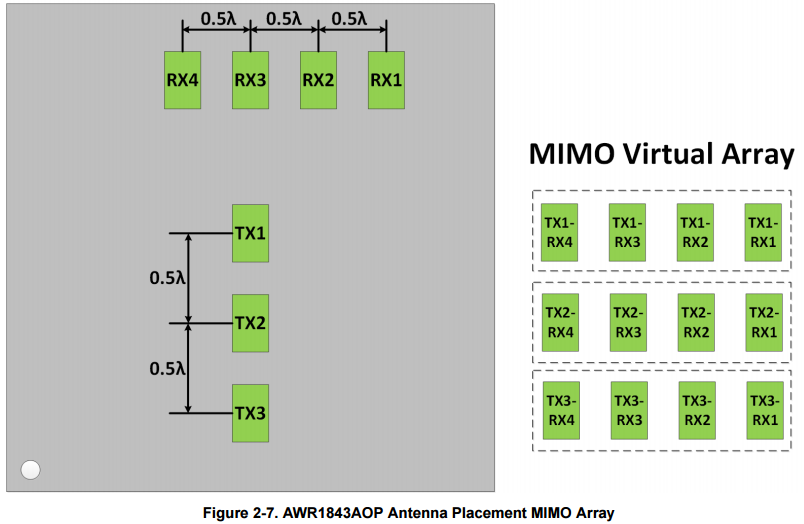출처 : TEXAS INSTRUMENTS AWR1843AoP EVM User’s Guide
여기서 MIMO는 Multiple-Input Multiple-Output을 말한다.
7개의 안테나를 활용하여 12요소의 가상 안테나 배열을 생성하여 2D가 아닌 3D, 또는 그 이상의 더 높은 공간 분해능, 각도 분해능을 얻을 수 있다.
😫 이 부분은 더 공부가 필요해서 이후에 다시 정리할 계획이다…
이처럼 안테나를 여러 개 활용하여 사용하게 되는데 지금은 개념과 안테나 원리에 대한 정리이므로 간단한 예시를 통해 이해해 보자.
송신 안테나(Transmitter, Tx) 1개와 수신 안테나(Receiver, Rx) 2개가 2차원 공간 상에 있는 상태이다.
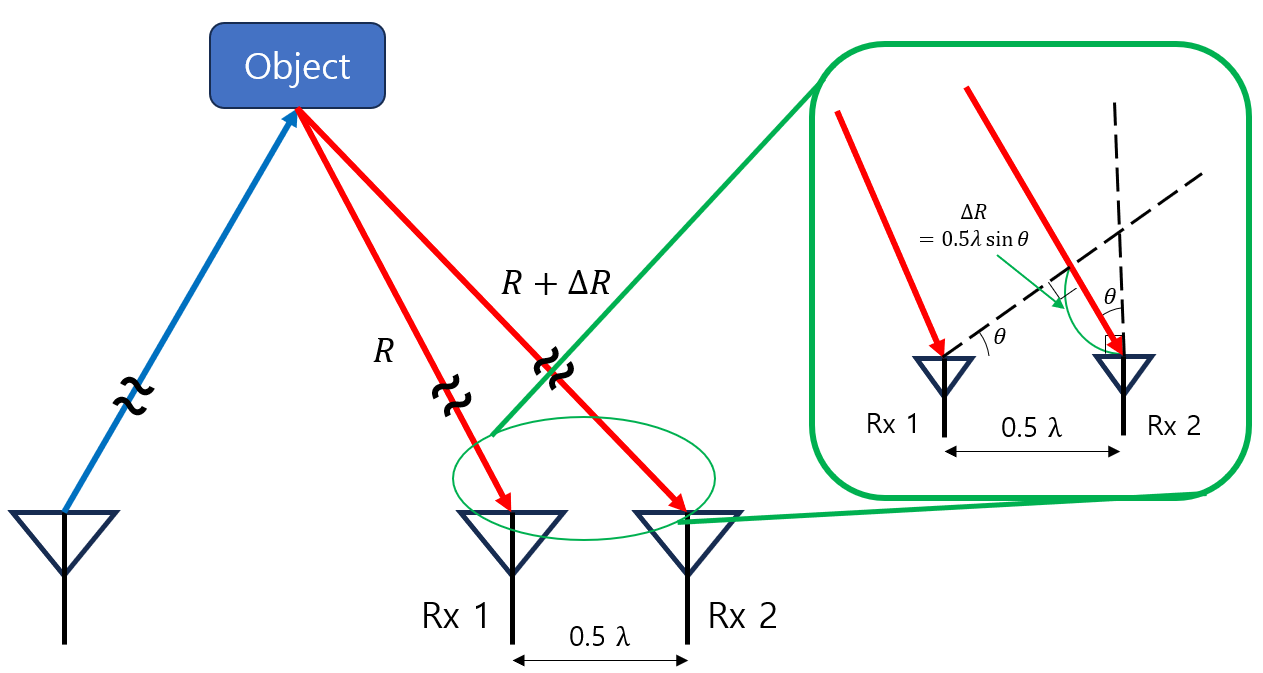각도 설염을 위한 그림 예시
이러한 경우 Rx 2 레이더가 Rx 1 레이더에 비해 $\Delta R$ 만큼 멀리 있기 때문에 그만큼 신호의 위상이 늦어진다.
이로 인해 수신 안테나간의 위상차이가 발생하게 되는데 이는 아래 식과 같다. \[ \frac{\Delta\Phi}{2\pi} = \frac{\Delta R}{\lambda} \] \[ \therefore \Delta\Phi = \frac{2\pi\Delta R}{\lambda} \]
또한 그림 상에서 확인할 수 있듯이 $\Delta R = 0.5 \lambda \sin\theta$ 이다.
이를 위상차이 식에 대입 후 각도에 대해 정리하면 아래와 같다.
\[ \Delta\Phi = \pi\sin \theta \] \[ \theta = \arcsin (\frac{\Delta\Phi}{\pi}) \]
수신 안테나 간의 거리가 $0.5 \lambda$ 일 경우 위 식처럼 깔끔하게 정리된다.
마치며
전자기파 송신 형태에 따른 분류 외에도 여러 분류방식이 있다.
- 빔 구동 방식
- 안테나 형태 : 위에 간단하게 기술하였음.
- 편파 응용 형태
- 용도
- 신호처리 방식
등 여러 분류가 있으나 이는 추후에 시간이 된다면 정리할 예정이다.
또한 이후 레이더 방정식과 안테나 배열을 통한 해상도 증가 등 좀 더 심화된 부분을 공부해나갈 예정이다.
참고자료
신의 눈, 레이더(Radar)
위키백과 - 레이더
[RADAR] 2. 레이다/레이더의 원리
정보통신기술용어해설 - 레이더 구분, 레이더 종류
Radar 센서
나무위키 - 레이더 반사 면적
Electronic Warfare and Radar Systems Engineering Handbook - Radar Cross Section (RCS) -
위키백과 - 도플러 효과
[레이더] 레이더의 분류
[레이더 시스템 설계 및 검증] LFM (Chirp) 파형의 이해
[레이더 시스템 설계 및 검증] LFM(chirp) 파형 Pulse compression (Convolution 방법)
자율주행 자동차 FMCW 레이다 (RADAR)
FMCW radar simulation in HFSS SBR+